An equation with the form ax^2+bx+c=0 is known as a quadratic equation. When plotted on a graph it will take the general shape of the graph seen below. The points at which the quadratic graph crosses the x-axis are known as the solutions of the quadratic equation.
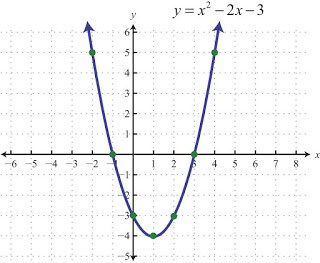
For this example, the quadratic crosses the x-axis when x=3 and when x=-1.
The quadratic formula is used to find the values that satisfy the equation.
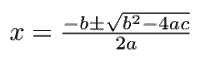
I wrote a python script which can find the solutions of these quadratics by using the quadratic formula.
import math
print "ax^2+bx+c=0"
a = float(raw_input("Please enter the value of a: "))
b = float(raw_input("Please enter the value of b: "))
c = float(raw_input("Please enter the value of c: "))
try:
x1 = (-b + math.pow((math.pow(b,2)-(4*a*c)),0.5)) / 2*a
x2 = (-b - math.pow((math.pow(b,2)-(4*a*c)),0.5)) / 2*a
except ValueError:
print "No real solutions"
exit()
print "X solutions: ", x1, ",",x2
The Quadratic formula has been wrapped in a try statement to prevent the program from crashing if a quadratic equation with no real solutions is entered. This would cause a crash as you would be trying to find the square root of a negative number which is not possible.